PLEASE NOTE: This article has been archived. It first appeared on ProRec.com in June 2000, contributed by then Media and Mastering Editor Lionel Dumond. We will not be making any updates to the article. Please visit the home page for our latest content. Thank you!
Hello, and welcome to the long awaited Part Two of “What’s your dB IQ?” I would sincerely like to thank all who have written me since the publication of Part One to tell me that you found it informative and helpful. If you’re jumping in fresh at this point, I heartily suggest you check out the original article first, as the material that follows here will build on the concepts introduced therein. Don’t worry… we’ll still be here when you get back!
Back in Part One I provided a detailed explanation of the term decibel, showed how the concept was derived, and presented examples of its use as a measurement of electrical power and voltage, as well as sound power, intensity, and pressure. I also wrote about standardized reference levels, and defined several decibel designations, such as dBspl, dBm, dBu, dBV, and so forth. There was also a brief exercise in conversion between different dB designations, presented as a discussion of nominal I/O levels between so-called “professional” and “consumer” gear.
As we press on undaunted, we’ll delve a little further into the topic of the decibel as it pertains to acoustics and audio engineering. We’ll do some dB calculations, develop a few handy rules-of-thumb (set off by borders, so they’ll be obvious), and get into some detail about weighted SPL measurements and other attempts to quantify the “loudness” of sound, especially as humans perceive it.
If you’ll recall, in the introduction to Part One we presented a few Decibel Brain-Teasers to test your knowledge of the topic. How many of you felt brave enough to tackle them then? For the ones that still remain unanswered, let’s roll up our sleeves, sharpen our pencils, and do a little cipherin’!
Decibel Comparisons
The sound of your sweetie whispering sweet nothings into your ear is 20 dB. The sound of your mother-in-law yelling at you is 60 dB. How many times louder is your mother-in-law than your paramour?
The real question here is, of course, “How many times louder is 60 dB than 20 dB?” Since we’re dealing with sound pressure levels here, the formula we’ve got to use is:dBspl = 20 log (P / R)
where P is the sound pressure level in Pascals (Pa), and R is a reference value (in the case of dBspl, .00002 Pa). This is the formula we use to express the difference between two absolute pressure measurements in terms of decibels (remember, a decibel is always a difference between two measurements!)
Let’s write down what we already know:20 log (PM / R) = 60 dB
20 log (PS / R) = 20 dB
where PM is the sound pressure created by your mother-in-law and PS is the sound pressure created by your sweetie. Therefore;20 log (PM / R) – 20 log (Ps / R) = 40 dB
20 log (PM / PS) = 40 dB
log (PM / PS) = 2 dB
(PM / PS) = 100
So, the answer is that your mother-in-law yelling at you is 100 times louder than the whispers of your lovely betrothed. (Please don’t invite me over for Sunday dinner, okay?)
There are a couple of things of note here. First, since the reference measurement R is a constant, and ends up dividing out of the equation anyway, it doesn’t really matter what the actual value of R is – in fact, it needn’t have appeared in the calculation at all. Second, there was never any need to derive the actual values of PM and PS – the problem was to determine how many times greater PM was than PS, so determining the value of the ratio (PM / PS) was enough. Knowing this, we could have started out with the equation20 log (PM/PS) = 40 dB
and arrived at the answer a bit quicker.
So, what does this tell us? Well, we know that if any two pressure measurements are 40 dB apart, that simply means that the larger one is 100 times greater than the smaller one. This hold true whether the two measurements in question are 60dB and 20dB, 50dB and 10dB, 110dB and 70dB, or whatever. Go ahead—try different values in the formula and see it for yourself!
Let’s take our new found decibel comparison skills and see if we can’t derive a few handy “rules-to-remember,” shall we?How many decibels louder is a sound if you crank it up to be twice as loud?
Easy! Let PA be the sound pressure level after you’ve cranked it up. Let PB be the original SPL. If (PA / PB) = 2, then20 log (PA / PB) = 20 log (2) = 6.0206 dB
which is damn close to (a mathematical term, meaning “approximately”) 6 dB. We can therefore say that, as a rule of thumb,An increase of 6dB of a sound means “twice as loud.”
This is a pretty handy thing to remember! If you are boosting a signal by 6 dB, that means you’re doubling the amplitude. Conversely,A decrease of 6 dB of a sound means “half as loud.”
By the same method, we can also derive the following:
| + 1 dB means about a 12% increase in SPL + 3 dB means about a 40% increase in SPL + 6dB means about twice as loud (200% of the original SPL) + 12 dB means about four times as loud (400% of the original SPL) – 1 dB means about 90% of the original SPL – 3 dB means about 70% of the original SPL – 6 dB means about half of the original SPL – 12 dB means about one-quarter of the original SPL |
In my opinion, these are values that a good engineer should know in his head. When you’re turning knobs and making adjustments to a signal based on dB values, it’s important to keep in mind what those values means in terms of actual sound levels.
Decibel Summation
There are two sound sources playing in a room: say, a drummer playing at 72 dB, and a guitar player playing at 66 dB. What is the loudness of the two playing together?
Remember, decibels are logarithmic units, and can’t be simply added together to produce a meaningful result. If we added 72 dB and 66 dB in the example above, we’d come up with a figure of 138 dB—which is approximately the volume of a jet engine at one meter! Remember that the upper threshold of human hearing is about 120 dB. Common sense tells us that either our answer is wrong, or we’re listening to one hell of a loud band.
There is a formula that allows us to combine decibels levels of different sounds from different sources in this manner. If the level of the first sound is represented as dB1, and the second sound, dB2:dB of combined sound level = 10 log (10 dB1/10 + 10 dB2/10)
If we plug in the figures in the example, we’d have the following:10 log (1066/10 + 1072/10) = about 73 dB.
There is something interesting worth noting about this equation: the result can never be higher than 3 dB above the higher of the two sound levels! In fact, if the two sound levels are the same (dB1 = dB2), the result will always be an increase of 3 dB. Also, the more the two readings differ, the smaller the increase in combined SPL will be, and of course the closer the combined result will be to the higher reading. There’s nothing magic about any of this – it can all be deduced from the equation. It would be a good exercise to plug in a few numbers and verify these rules for yourself.
Let’s summarize these general rules:
| Combining two different sounds of the same level results in an increase of 3 dB. The smaller the difference in level between two sounds, the greater the increase in their combined SPL will be (to a maximum of 3 dB). The greater the difference in level between two sounds, the smaller the increase in their combined SPL will be. |
But wait – haven’t we already said that “twice as loud” means an increase of 6 dB? There appears to be a contradiction here, but really there isn’t. When we talked before about a 6 dB boost in a sound being twice as loud, we were in fact talking about a single sound being boosted from it’s previous level. The above formula holds true only when the two sounds being compared are different. It’s a subtle but crucial distinction. The formula is useful, because when we talk about sound levels combining in this manner, we’re almost always talking about different sounds. The fact is that if the two sounds are similar enough (i.e., phase correlated) the actual increase will be higher than predicted by the formula—and if the two sounds are the same, the increase in level can in fact be up to 6 dB.
You’ve scored some sweet tix to a Pearl Jam concert, where the SPL is 120 dB. As you’re waiting in the interminably long line to get out of the parking lot after the show, you crank their latest CD on your car stereo at a level of 100 dB. How many car stereos played at that volume would it take to produce the same SPL as the concert?
Here we’re combining not only two, but several, different sound sources to determine the combined result; however, the procedure is the same. Since each car stereo is playing at the same volume (100 dB), let’s use the following equation:120 dB = 10 log (n * 1010)
where n is the number of car stereos that would combine to produce a result of 120 dB. Solving for n produces a result of 100. That means it would take 100 car stereos playing together at 100 dB to produce a combined SPL of 120 dB!
Does this result surprise you? It shouldn’t! From the rules of thumb we developed earlier, we know that two stereos playing together at 100 dB would be 103 dB. Applying the formula above, we find that adding a third stereo to the first two would produce a result of 104.8 dB (an increase of only 1.8 dB). Adding the fourth would make 106 dB, the fifth 107 dB, the sixth 107.8, and so on. You can see that each additional stereo makes less and less of an increase to the total result—which not only follows our rule, but should make intuitive sense based on your own everyday observations. When you yell at a small party, everyone hears you; when you yell at the same volume at a ballgame, you don’t add much to the overall volume of the crowd!
How much louder is a 100-watt guitar amp than a 50-watt guitar amp?
Hey… after all this mathematical gymnastics, this one is a piece of cake! We know that watts are a measurement of electrical power. You’ll recall the dB formula for power measurements isPower dB = 10 log (P1 / P2)
where P1 and P2 are the two readings being compared. You can already probably figure out in your head that the answer to the problem is 3 dB.10 log (100 / 50) = 3 dB.
Let’s Join the Real World Now
So far, all the information we’ve presented about decibels as they apply to the behavior of sound has been purely theoretical. We’ve talked about the sound pressure level without respect to frequency, which is to say, we’ve been using an unweighted system of decibel measurement. However, studies done over the years—using real people listening to real sounds—have revealed that the perceived loudness of a sound depends on the frequency of that sound. In other words, the frequency response of the ear isn’t flat at all, but is more sensitive to sounds in the middle of the audible spectrum than it is to low-frequency or high-frequency sounds. If you were to plot a frequency response graph of the typical human ear, you’d have a graph showing “3 dB down” cutoff frequencies at about 500 Hz on the low end, and 8 kHz on the high end. You’d also see a gentle yet pronounced “presence peak” at around 4 kHz, which indicates that the ear is most sensitive to sounds in that range.
Unfortunately, that’s not the only fly in the ointment we have to deal with, because it’s also true that the way in which the ear responds to various frequencies is dependent on the loudness of the sound itself. In other words, the ear’s frequency response is flatter for loud sounds, and less flat when the sound is relatively soft.
Back in 1933, a couple of scientists named Fletcher and Munson did experiments on all of this stuff and developed a series of curves that very closely approximated the response of the human ear with respect to both frequency and loudness. These curves are sometimes referred to as the Fletcher-Munson loudness curve, or more commonly the equal response contour. (If you’ve worked with audio technology in any depth in the past, these are probably both terms you’ve already heard.)
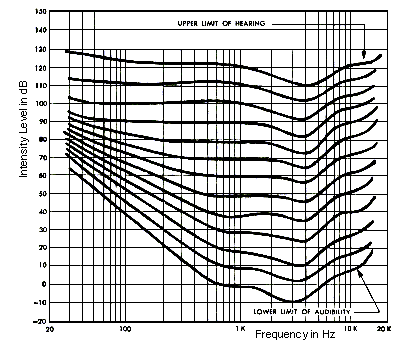
These curves represent a plot of sound pressure levels of pure sine tones that are generally perceived as being equally loud. (They are, in fact, the inverse of the human ear’s frequency response graph.) As an example, take a look at the sixth curve from the top. It shows that if a 1 kHz sine tone is played at 70 dB, a 70 Hz tone would have to be played at 80 dB to be perceived as equally loud; a 16 kHz tone would have to be played at 90 dB to be perceived as equally loud, and so forth. Note how the equal loudness contour is flatter for louder sounds and much less flat for softer sounds.
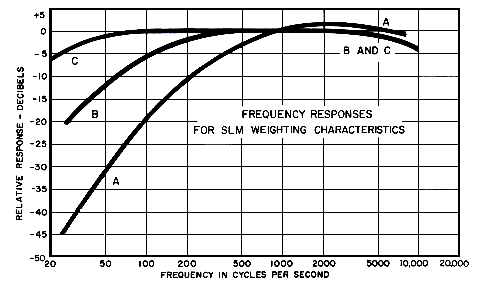
A few years after Fletcher and Munson published their results, acoustical engineers developed decibel weighting systems to compensate for the ear’s imperfect response. Nearly all sound level meters incorporate electronic filters that reflect the now-standardized decibel weighting systems. The three most common weighting systems are A-weighting, B-weighting, and C-weighting, which attempt to compensate for soft, medium, and loud sounds respectively. By far, the most common designation you’ll find is the A-weighting, designated as dbA or dB(A). The A-weighting system has, over time, been adopted by government agencies like the FAA and the EPA, and is used for nearly all legislative and other “official” purposes, such as noise control ordinances and the like. B-weighting is rarely used nowadays. C-weighting, which most closely corresponds to the unweighted measurement of SPL, is occasionally used for sound levels exceeding 100 dB.
The graph below shows the weighting curves used for most sound level meters.
Conclusion
There are several other factors which color the way in which humans perceive sound, all of which complicate to some degree any attempts to accurately express sound levels in terms of decibels. Frequency and loudness are not the whole story! These other factors include the sound’s waveform, complexity, spectrum, harmonic content, duration, spatial properties, attack and decay characteristics, and the simultaneous presence of other sounds, to name a few. The study of how humans perceive, react to, and interact with music, noise, and sound is called psychoacoustics. Many in this field have tried to come up with systems to accurately quantify various aspects of sound perception, and the decibel is among the most important tools they use for this purpose.
As audio engineers, producers, technicians, and musicians, a clear understanding of the decibel is important to us as well, as we pursue our endeavors in the technology of sound. Again, I hope this Part Two of “What’s your dB IQ” (along with Part One, of course) was helpful in helping to develop that understanding.
And once again… happy dBs!