PLEASE NOTE: This article has been archived. It first appeared on ProRec.com in May 1998, contributed by then Media and Mastering Editor Lionel Dumond. We will not be making any updates to the article. Please visit the home page for our latest content. Thank you!
Part Two: Whatchoo Talkin’ ‘Bout, Lionel?
Welcome back! As you will recall, in Part One of this article, I introduced this discussion of EQ on a mainly conceptual level, and gave an example of the most common role of EQ in modern pop recording — as a tool to separate timbres across the frequency spectrum in a multitrack mix. While I tried to keep it as simple as possible, I did throw out a few technical terms and concepts with which you may not be familiar — things you’ve probably heard about, but may never have fully grasped.
The concept of audio equalization — a process by which a specific part or parts of the audible frequency spectrum are either cut or boosted, in order to change a sound — is very simple. The implementation of that process in the studio, however, is a little more involved. In Part One, we more or less focused on the “whys” of EQ. Here in Part Two, let’s delve into the “hows” and “whats” a little more.
In the modern studio, there are a ton of EQ options at our disposal. There are dedicated outboard hardware-based equalizers, and there are equalizer software plug-ins. There are solid-state equalizers, and there are tube-based equalizers. Practically every mixing console has some form of EQ on each channel strip. Some EQs are graphic, some are parametric, some are semiparametric (also called sweepable) and a few — especially those of the software variety — are paragraphic, a hybrid implementation that combines various features from the other types. Heck, even your home stereo system probably has “treble” and “bass” controls — and that too is a very basic implementation of EQ technology.
The whole purpose of an equalizer is to get rid of frequencies in a sound we don’t want, and to enhance the frequencies we do want. So, it makes sense that we’ve got to provide at least two parameters — one, what frequency do we want to affect; and two, how much do we want to affect it? The “how much” is generally expressed in terms of decibels (dB) a concept which most engineers have at least a faint grasp on. <chuckle>. (Maybe I’ll explain dBs in a future article?) So, for now, let’s look at the “what” parameters, how they’re expressed, and what they mean.
Ouch, That Hertz
As you know (please, tell me you know this) sound is vibrating air. The frequency of a sound is technically expressed in hertz — the number of times a particular sound (or a particular portion of a sound) makes the molecules in the air vibrate every second. Hertz is abbreviated “Hz” and is so named after a very cool guy, whom I believe retired from acoustic research to start a car rental company (just kidding). One thousand hertz is a kilohertz and is abbreviated “kHz”, or on occasion as simply “k”. So from now on, if you hear someone say, “the vocals need some articulation, let’s boost a little around 4k,” you know that “4k” means 4,000 Hz.
The human ear is only capable of hearing sounds from about about 20 Hz to about 20 kHz. This range, comprising about 10 octaves in musical terms, is called the audible frequency spectrum. There are sounds that extend well beyond that range that your dog can probably hear just fine, but we don’t concern ourselves with those because, well… dogs don’t buy records, do they?
The reason I was careful to say “a portion of a sound” back there is because just about all sounds contain several frequencies — in fact, usually many thousands of different frequencies, each at varying amplitudes (loudness). A simple sine wave is the only type of sound that contains one and only one frequency. In fact, a man named Fourier once postulated that any complex sound (one containing many different frequencies) can be represented as a collection of many, many simple sine waves added together. It is this theory upon which is based a mathematical algorithm we call a Fast Fourier Transformation (FFT). Spectrum analyzers, which provide a visual representation of which frequencies at what amplitudes a sound is made of, operate using FFT algorithms.
Yes, but of course by now, your eyes are glazing over and your brain is going into vaporlock. Just a bit of interesting digression back there — sorry, I couldn’t help myself. The whole point I was trying to make is that 1) there are many portions of a sound that are spread all across the frequency spectrum, 2) that the amplitudes of these various frequencies vary along the spectrum, and 3) each of these frequencies can be pinpointed and expressed in terms of Hz. It is precisely this mix of frequencies and amplitudes that determines the timbre of a sound, and allows the ear and brain to distinguish between, say, a violin sound and an oboe sound. You will sometimes hear the term fundamental frequency used, which is generally the loudest frequency present in a sound, that which determines its pitch. For example, if I play a middle A on a piano, though that sound is made of many frequencies at varying amplitudes, I know that the fundamental is at 440 Hz.
To attain the status of Super-Duper Ace Engineer / Producer / Babe-Magnet to which you truly aspire, it’s important to learn, over time and with practice, the “sound” of each frequency and the number of Hz that corresponds to it. To be able to identify frequencies and frequency ranges by ear is as vital a skill to an engineer, as being able to play tunes by ear is to a musician. Remember that! As an experienced recording and mastering engineer, I’ve developed the ability to hear a track or a mix and pretty much tell by ear what frequencies I’m going to need to deal with, so I know straight away what to grab for. I practice and hone this skill every chance I get, and I constantly get better at it the more I do. You should do the same — it’s a valuable skill to have!
You should also be familiar with the frequency ranges of various instruments that you’re likely to come across. For example, I know that the fundamental frequency of the lowest note on a piano is 28 Hz, and the highest note is at 4186 Hz. These are just things you should make yourself aware of.
Dirty Used Q-Tips
We’re still addressing the first important EQ parameter — what to affect. We have learned to express it in terms of Hz. But that’s not the whole story.
You see, this is the real world. (Yeah, I’m so sorry to burst your bubble. Suck it up… I have to live here, too.) And in the real world, with real sounds, made up of scads of real frequencies, it would usually make no sense to merely boost or cut a single frequency. Most times, you’d probably want to alter a fairly wide range of frequencies. And besides, in the real world, equalizer circuits and/or algorithms just aren’t that precise, anyway. And can you imagine an equalizer with thousands and thousands of sliders on it, one for each possible frequency? It would be hell to try to fit that in your rack, wouldn’t it?
So, when you use an equalizer to boost or cut a portion of a sound at a certain frequency, you are also boosting or cutting frequencies nearby, on either side of that frequency. On an equalizer, that “certain frequency” is called the center frequency. Just how much of the spectrum on either side of the center frequency is being boosted or cut along with it, is determined by the bandwidth.
Okay… so when you cut or boost using an equalizer, you are affecting a range, or “band”, if you will, of frequencies. It could be a narrow band, or a wide band. Pretty simple, isn’t it? But the terms in which bandwidths are commonly expressed can be a little tricky to understand.
Often, you will hear the term Q used. Q is a way of describing the shape of the EQ response curve as the ratio of the center frequency to the difference of the upper and lower frequencies that are being affected. The upper and lower frequencies are defined to be the points at which the cut or boost in question is 3 dB less than is being boost or cut at the center frequency. In other words, lets say for example that the center frequency is 6 kHz, and that we are boosting 12 dB at that point. Let us also suppose that the EQ filter curve is shaped such that we are boosting 9dB at 4 kHz and also 9 dB at 8 kHz. This would lead to the following:
……..6 kHz
Q = ————- = 1.5
….8 kHz – 4 kHz
Since the bandwidth control on an equalizer is often labeled by Q, it is often more useful to derive the bandwidth for a given equalizer Q setting, since it’s the bandwidth that you’re actually interested in. So therefore, using the above example, if you dialed in a center frequency of 6 kHz and a Q of 1.5, your (+/- 3dB) bandwidth extends about 4 kHz around the 6 kHz center frequency — from 4 kHz to 8 kHz, or about one octave.
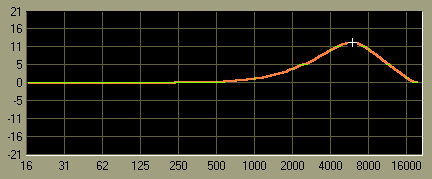
12db boost with Q=1.5
Now, let’s say you move the center frequency to 12 kHz and keep the Q at 1.5. The range of frequencies being affected by +/- 3 dB is from 8 kHz to 16 kHz — still one octave. In fact, no matter where you set the center frequency, a Q of 1.5 will give you a bandwidth (by the +/- 3dB definition) of one octave.
Why am I boring you stupid with all of this mind-numbing silliness? Because, a lot of people find Q confusing and ask me about it. So, now their curiosity has been satisfied. A lot of others probably skimmed over that section pretty quickly and didn’t absorb much. Good for them! Q is not a musical concept at all; it is basically an geek term made up by engineering dweebs who have no life. You know how I hate rules, but now, I am about to lay down a rule and you best remember it. Cool people express equalizer bandwidth in terms of octaves, not Q. Don’t ever say in a professional studio, “I think we ought to boost that track at 8 kHz with a Q of three.” People will think you’re a dork. No one knows or cares what the hell a “Q” is. “Half an octave”, now that’s something a musician can relate to.
For reasons that are too complex to go into fully here (and besides, I’m sick of talking about it) the musical effect of an EQ cut or boost can be radically altered if the Q is kept constant while the amount of cut or boost is changed. This is related to the fact that Q’s real purpose, from a design standpoint, is to describe the shape of the EQ curve — not to delineate true perceived bandwidth. In order to maintain a constant musical bandwidth, the shape of the EQ curve (and thus the Q value) must change radically when amplitude changes. This is why, from a practical standpoint, the true definition of Q is rarely if ever used in its strictest sense in equalizer implementation. There is one famous brand of equalizer that claims to sound better because it uses “constant Q” circuitry, when in fact it does just the opposite! In fact, better equalizers allow the actual Q to vary as the amplitude is varied, so that bandwidth remains roughly the same — which creates a more musically pleasing effect, and sounds more accurate to our ears. So, as you can see, the whole concept of Q is pretty well misused, abused, and poorly understood, anyway. So why memorize it? Just remember this: the higher the value of Q, the narrower the range being affected; the lower the Q, the wider the range being affected. That’s all you really need to know.
Practically speaking, I find that one octave or so is a good bandwidth to start out with for most general EQ tasks. An octave is generally narrow enough to get close to the frequencies you’re after, while wide enough to not have too radical an effect. A wider bandwidth (two or three octaves) is good for less specific overall coloration A narrower bandwidth (1/3 octave or less) is generally used for cutting problem frequencies, such as line noise, or for feedback control in a live sound situation.
Shapes and Sizes
In the world of humming electrons (or, in the case of software-based EQs, humming ones and zeroes), all of this bandwidth and frequency and dB manipulation stuff is accomplished with the use of filters — either electronic filtering circuits, or binary filtering algorithms, as the case may be. The bell-shaped EQ curve as described above, with a center frequency and bandwidth, is achieved using a parametric filter (sometimes called a band-notch filter). While this is the most commonly encountered type of filter, it’s by no means the only kind you’ll find out there. You see, these wonderfully creative tweaky filter designers have come up with a lot of other types of filters that can be used for EQ as well. In addition to parametric filters, there are bandpass, lowpass, highpass, low-shelf, and high-shelf filters, too. We’re going to discuss them briefly, but tread carefully here — a lot of these terms are bandied about rather indiscriminately, and some are used interchangeably when they really shouldn’t be. Consider yourself warned.
Bandpass filters are basically the opposite of parametric (band-notch) filters. As we’ve discussed, a parametric filter boosts or attenuates a range of frequencies around a certain center frequency. The bandpass filter allows us to select a certain range of frequencies and leave it alone, while attenuating everything else outside that range. In other words, it lets the chosen band of frequencies “pass” through unaffected — hence the name. Pretty clever, eh?
The terms lowpass (sometimes called high-cut) and highpass (sometimes called low-cut) derive their names in a similar way. A lowpass filter set at a particular cutoff frequency will lower the amplitude of all frequencies above the cutoff, letting the “lows pass” through unaffected. Likewise, a highpass filter allows the high frequencies to pass, attenuating all frequencies lower than the cutoff frequency. It might be useful to think of a lowpass filter as the “high side” of a bandpass filter, and conversely a highpass filter as the “low side” of a bandpass. In fact, this is how many hardware EQs work — they use high- and lowpass filters together to create a bandpass.
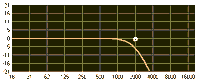
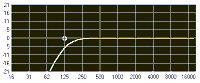
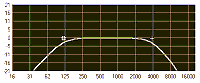
You may hear the terms lowpass and low-shelf used interchangeably, as well as highpass and high-shelf. While very similar in function, this isn’t technically correct. As we’ve already seen, a highpass filter cuts all frequencies below a given cutoff frequency, while a high-shelf filter does just the opposite — it boosts all frequencies above the cutoff point. If you think about it, this is a very similar process. In fact, it’s possible to make a highpass filter act somewhat like a high-shelf filter (and vice-versa) by engaging the highpass filter and then boosting the equalizer’s overall output level. And, conversely, a low-shelf filter boosts all frequencies below the cutoff point. Of course, in a similar fashion to that described above, it’s possible to make a lowpass filter act like a low-shelf one.
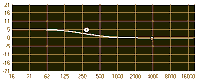
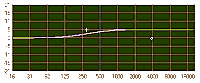
High- and lowpass and high- and low-shelf filters are sometimes collectively referred to as shelving filters. Of course, with shelving EQ such as this, it makes no sense to speak in terms of “center frequency” and “bandwidth”. Instead, we define these parameters in terms of cutoff frequency (sometimes knee frequency) and rate (often referred to as slope). The rate of a shelving filter is expressed in dB/octave. For example, if a lowpass filter has a cutoff frequency of 2 kHz, and the rate is 6 dB/octave, then at 4 kHz, the amount of cut will be -6 dB; at 8 kHz, the amount of cut will be -12 dB; at 16 kHz, it will be -18dB, and so on.
That’s a lot of filtering options, isn’t it? I suggest that you become comfortable with all of them and understand how they work. It can be tricky, because practically speaking, the sonic differences among different filters can be pretty subtle, and the same filter circuits are often pressed into double or even triple-duty in the same box. In fact, if you think about it carefully, you’ll see that it’s possible for a simple two-filter system — highpass and lowpass — along with adjustable output gain, to recreate all the other types — parametric, bandpass, high-shelf, and low-shelf EQ. In fact, this is exactly how a lot of cheap EQ boxes work — a few simple circuits, each designed to do multiple tasks.
Gettin’ it Done
So far, we’ve outlined the basic technical concepts — what frequencies to affect (in terms of center frequency and bandwidth, or cutoff frequency and rate), and how much to affect them (in terms of dB). We’ve also touched upon different filter designs. Exactly how these parameters are addressed and controlled in real-world EQ design varies greatly, usually determined by how and which EQ parameters can be user-adjusted, and which are fixed. Let’s examine some of the more common EQ implementations.
Fixed EQ
This is the type of EQ you’re likely to find on the vast majority of home hi-fi preamps, and on the channel strips of the cheapest mixers. Here, you only have the option of controlling “how much” — the “what” is fixed and is not adjustable.
These usually consist of two or possibly three rotary pots. The high (or “treble”) and low (“bass”) knobs are generally shelf-type filters with fixed cutoff frequencies (usually at about 100 Hz and 10 kHz or thereabouts) and pretty generous slopes. The “mid” control (if there is one) is a band-notch filter with a fixed center frequency and bandwidth, usually at least a few octaves at around 2 kHz or so.
Needless to say, this is the least flexible of all the types of EQ, and are good for little else except very broad tone-shaping.
Semi-Parametric (Sweepable) EQ
This is a major step up from fixed EQ. While the bandwidth is still fixed, the center frequency can be adjusted; usually along a very wide range. This is what you’ll usually find on nearly any decent, mid-priced mixer. For example, the channel strips on a Mackie 1604 has fixed high and low controls, but a semi-parametric mid-band control.
This is a great tool to have, as the ability to pinpoint a specific frequency has tremendous advantages. Try this trick sometime — if you are trying to hunt down a specific frequency on a track (such as the attack on a guitar, the snap of a kick drum, or the beefiness in the bass), run the track through a semi-parametric EQ and boost the gain control full up. Then sweep the center frequency s-l-o-w-l-y from its lowest to highest point. If you listen carefully, the frequency you’re seeking should jump right out at you! Once you’ve found the desired frequency, then back off on the gain control, adjusting it to taste or as necessary to achieve the desired result.
Parametric EQ
This is the most adjustable and flexible type of EQ, and can pretty much address almost any EQ task. With a parametric EQ, gain, frequency, and bandwidth can each be adjusted on its own, independently of the others. The sweeping trick discussed above is often used with parametric EQ, with the added advantage that the bandwidth can be set up to affect a very wide range of frequencies around the center, or a very narrow range, depending on your needs and the specific application. With a parametric EQ, you can do some powerful and very specific tone coloring. If you refer back to Part One of this article, where I walked you through some EQ mixing fundamentals, you’ll see how useful a parametric EQ could be for this purpose — with total and ultimate EQ control right at your fingertips, making the pieces of a mix fit together is much, much easier and far more effective!
The more expensive and nicer recording consoles usually have at least one band, and sometimes two or more overlapping bands, of parametric EQ — if not on all channels, then at least on some of them. Of course, not everyone has the luxury of working on one of these babies. If not, I strongly recommend that anyone truly serious about recording get their hands on at least one — if not a couple — of top-notch, outboard multiband parametric EQs. Be warned; the good ones (really, the only kind worth having, right?) are not cheap; but the flexibility, control, and incredible array of EQ options you’ll have at your disposal will be worth it.
Graphic EQ
This is the type of equalizer that is familiar to most people, and is the easiest and most intuitive to operate. It is somewhat similar in operation to fixed EQ in that bandwidth and center frequencies are fixed, but instead of having only two or three rotary controls, it sports many sliders (usually ten or more) at many different frequencies spaced evenly across the audible frequency spectrum. The range of boost or cut possible is usually at least +/- 12 dB, but better units can go +/- 18 dB or even higher. Just by looking at the slider controls on an graphic EQ, you can pretty much tell what the resulting EQ curve looks like.
The bandwidth of each slider control on a graphic EQ is dependent upon the number of sliders it has. A graphic EQ is set up so that it reaches from the lowest to the highest point in the spectrum. As we said earlier, the audible spectrum is about ten octaves wide. So, if we have a graphic EQ with ten sliders on it, what would the bandwidth of each slider be fixed at? Hmmm… this is a hard one, eh? Take your time. Okay…. time’s up! The answer is that each slider has a one octave bandwidth. No duh.
Here’s your extra credit question: if you wanted to build a graphic equalizer that could provide even more precise control — say, a one-third octave bandwidth for each slider — how many sliders would you need? Did you say “thirty?” WRONG! It’s actually thirty-one! Traditionally, EQ manufacturers sneak an extra slider into the one-third octave graphic EQ, which allows them to effectively cover just a little bit more ground than you usually can with a ten-band EQ. The 31-slider configuration is pretty much an iron clad standard — you will not see a thirty-band graphic EQ anywhere, trust me on this.
Besides one octave (ten-band) and one-third octave (31 band) graphic EQs, you’ll occasionally run into a 15-band EQ out there. If you’ve been paying attention (hey you in the back, face forward and be QUIET!) you should be able to deduce that each slider on a 15-band EQ would have a bandwidth of two-thirds of an octave.
Paragraphic EQ
With the advent of digital display technology and computer-based recording and processing, it has become possible to combine many of the best features of both the parametric and graphic equalizer. This has brought us the relatively recent hybrid beast that we call the paragraphic EQ. The paragraphic EQ doesn’t differ a single bit from the parametric EQ in terms of sound, controllability, or flexibility of purpose; but only in the way the user interfaces with it.
Traditionally-designed, hardware based EQs are pretty much limited to the use of real-world, tactile controls — buttons, knobs, dials, and what not, that you can physically grab with your fingers and twist and tweak to your heart’s content. There’s a lot to be said for this; however, it has its drawbacks, too. With a parametric EQ, usually consisting of an array of knobs, you don’t receive much visual feedback as to what you’re doing — as you change the settings, the sound changes, but the knobs just sit right there. The sliders on a graphic EQ provide a much better visual representation of the EQ settings you’ve made; but still, bandwidth and frequency for each slider is fixed, and there are other, physical limitations as well — for instance, you can’t move the sliders around, or make them appear in a different order if you want to.
However, with software-based EQs and EQ plug-ins — and increasingly, on outboard units with digital control via LCD screens and the like — these physical limitations don’t apply any more. The sky is pretty much the limit here — using the powerful graphical interfaces possible on today’s computer displays, it’s possible to make EQ controls pretty much look like whatever the developer dreams up. Many of the cleverer companies out there have taken advantage of this to create EQs that still contain all the power and control of a parametric EQ, but that present an intuitive look and feel, much like a graphic EQ.
What’s A Head?
Next month, in Part Three of this article, we’ll talk more about paragraphic EQ as ProRec hosts the Great Software EQ Shootout. We’ll delve into some cool software-based EQs from companies like Cakewalk, Sound Forge, Waves, and Syntrillium. We’ll twist, torture, and pummel them until they beg for mercy, and then we’ll rate them for sound quality, ease of use, and abundance of cool features. And, if anyone reading this has a spare $4,000 Avalon tube EQ, or better yet, a vintage Weiss or a cool Neve console EQ sitting around their place, feel free to send it along and I’ll review that, too <ha ha>.
Until next time… here’s hoping that all your EQ experiences are happy ones… and don’t ever forget… the music’s the thing!