PLEASE NOTE: This article has been archived. It first appeared on ProRec.com in April 1999, contributed by then Media and Mastering Editor Lionel Dumond. We will not be making any updates to the article. Please visit the home page for our latest content. Thank you!
Probably one of the most misunderstood concepts in all of audio science is that of the decibel — what it means, and what it doesn’t mean. This really isn’t very surprising. Most books you’ll find on audio production gloss over the subject, offering a rudimentary explanation at best. What’s worse, you’ll often see the term “dB” bandied about with little consideration given to the context in which it’s being used — are they talking dBu, dbV, dBm, dbVU, dBFS, dBspl, or what? And being a rather complex concept, the term doesn’t lend itself well to a one or two sentence glossary-style entry. For example, if you look up “decibel” in a book, you might read something like “the smallest increment of sound which the human ear can detect” — which only happens to be true in general, but certainly isn’t an accurate definition by any means.
What’s more, this lack of understanding isn’t limited to beginners. There are folks I know who’ve worked in this field for a long time who aren’t clear on the whole thing — even though many of them think they are.
A keen grasp of all this decibel stuff is crucial to the understanding of just about every other audio concept there is. So my question to you is this: how well do you know your stuff? Think you’ve got it all down? Want to find out?
Okay, hotshot… it’s pop quiz time. Sharpen a number-two pencil and let’s go.
1. The sound of your sweetie whispering sweet nothings in your ear is 20 dB. The sound of your mother-in-law yelling at you is 60 dB. How many times louder is your mother-in-law than your paramour?
2. You’ve scored some sweet front-row tix to a Pearl Jam concert, where the SPL is 120 dB. As you’re waiting in the interminably long line to get out of the parking lot after the show, you crank their latest CD on the car stereo at a level of 100 dB. How many car stereos played at the same volume would it take to produce the same SPL as the concert?
3. There are two sound sources in a room: say, a drummer playing at 72 dB, and a guitar player playing at 66 dB. What is the loudness of the two playing together?
3. What is the difference in dB between the nominal output levels of “consumer” gear (-10 dBV) and “professional” gear (+4 dBu)? (Hint: It’s not 14 dB.)
4. What’s the dynamic range of 16-bit digital audio in dB? Of 24-bit digital audio? Could you figure out the dynamic range of a 21-bit digital audio system?
5. How come you can go over 0 dB on an analog two-track, but can’t go over 0 dB on a DAT?
6. How much louder is a 100 watt guitar amp than a 50 watt guitar amp?
If you can answer these questions with ease, then this article wasn’t written for you. But, if you found yourself scratching your head and saying “huh?”, read on. Beware the road signs that read “Caution — Math Ahead!” I’m sorry about that, but it’s truly not possible to gain a through understanding of dBs without a little cipherin’ along the way. If you are one of those people whose eyes glaze over when faced with a pageful of equations, fear not. I’m right here beside you! Stick with it, reread it a couple of times if you have to, and before too long the light bulb will come on, I promise you.
Oh, and one more thing — if you want to follow along with your own calculator, make sure you have a scientifical-type one that has a “log” function. Be careful not to get the “log” button (the function that computes the base-ten logarithm) confused with the “ln” button (the function that computes the natural logarithm, which is a kind of a log that marches to a whole different rhythm.)
And so, come with me now if you will, as we step through the looking glass into the Wonderful World of the Decibel — where subtraction is division, rulers are longer on one end than the other, and nothing is as it seems…
Logarithmic Scales — the Kind You Can’t Play on a Piano
The term dB has meaning in all kinds of scientific measurement — from sound, to electrical or mechanical power, to voltage, and so on. The decibel scale is an example of a logarithmic scale. Other examples of logarithmic scales used in scientific measurement are the Richter scale (used to denote the energy of earthquakes) and the pH scale (used to indicate the concentration of hydrogen ions in a solution).
Why do scientists use logarithmic scales? Well, one thing you have to remember is that scientists — much like guitar players — like things easy! And when you’re dealing with a large range of numbers that have a bunch of zeros before or after the decimal point, using logarithms makes those numbers a whole lot easier to work with and compare to each other.
Let me give you an example. Let’s say you’re a scientist in the way-back old days. You’re observing some phenomena dealing with sound. You’ve performed a few experiments, and have taken some measurements about the intensity of sound. You know that sound is the movement of energy, and that sound intensity is the amount of energy passing through a given area per unit of time:
Intensity = Energy / (Time * Area)
Since we know that the ratio Energy / Time is equal to Power (think hard… remember your high school physics?) we can say:
Intensity = Power / Area
And so, since sound intensity is the amount of sound power per unit of area, and we scientists measure power in watts, let’s express our measurements in watts per square meter (W/m2), shall we? Okay, so far, so good….
Now suppose, if you will, that you’ve found that the smallest sound intensity that most people can hear is .000000000001 W/m2. You also discovered that the intensity that makes people start to wince in pain is 1 W/m2. Of course, you’ve taken a bunch of measurements in between as well, like .000792710162 and .000006288415. Just try conveniently comparing those numbers! Quick — what’s the difference between .000792710162 and .000006288415 ? Try figuring that one out in your head!
Let’s see if we can make these numbers smaller and easier to work with. Instead of using these unwieldy numbers in their raw form, let’s try taking the base-ten logarithm of these numbers, and working with those results instead. It just so happens that:
log ( .000792710162) = -3.1
log ( .000006288415) = -5.2
Now… doesn’t that look a whole lot less daunting? We can easily see here that the difference in the logarithms of these wacky figures, is an easy-to-handle “2.1”. Yes… but 2.1 what? What are we going to call this “difference” number? You suddenly come up with a brilliant idea — you’ll call it a Bel, after your boyhood hero, Alexander Graham Bell! (Alexander Graham Bell was your boyhood hero, wasn’t he? Come on, work with me here, people…)
You take all this into your boss, hoping for a pat on the back and maybe even a big raise. He looks at it and says, “Hmmm… I like it. Good work. But I don’t like that messy decimal point. Get rid of it!”
So, you decide to change your units a little bit, by multiplying both sides of your equations by 10.
10* log ( .000792710162) = -31
10* log ( .000006288415) = -52
But then, your difference isn’t 2.1 any more, it’s now 21. The units are now one tenth the size of the Bel you came up with before, so you decide to call this “new” difference unit a decibel, or dB for short. A decibel is one tenth of a Bel.
But gee… why stop there? Remember, we’re lazy scientists here. Can’t we somehow make this stuff even easier? We sure can, because we know that our friend the logarithm can do a cool trick — it can turn subtraction into division!
10* log (x) – 10* log (y) = 10* log (x/y)
In other words, we don’t have to take the logarithms of both numbers. We can simply derive the ratio of the two numbers, and only have to do one logarithm calculation, instead of two! (You have to remember, this was long before scientific calculators were invented — scientists had to use slide rules to figure all this stuff out, so the fewer logarithm calculations, the better!)
10* log (.000792710162 / .000006288415) = 21 dB
So, now you know why scientists like to use logarithmic scales — when you’re dealing with a huge range of numbers, it just makes comparing things a whole lot easier!
The Decibel Difference — Nothing Else Compares!
Cool. Now we have a convenient way of comparing two unwieldy numbers. But — and this is a very crucial point to understand — the number we always come up with is not an absolute value, but is a comparison between any two measurements (or, more precisely, the difference in their logarithms, times 10). Remember, we came up with this decibel thing to show the difference between two measurements. Therefore, it makes no sense unless you’re dealing with two numbers, right?
Let’s see if we can’t refine our system a little more…
So far it’s been a pretty hard day; so you decide to knock off work early and have yourself a couple of brewskis on the ol’ laboratory expense account. As you’re holding down a barstool at your favorite local pub, you find yourself starting to scribble on a napkin.
Suddenly, you shriek out loud, “Eureka! How about, instead of dividing two measurements we want to compare, that we just pick some reference number that will remain constant, and divide all our raw measurements by that number? The results would still be the same!” Here’s what you scribbled on your napkin. Let’s call the reference number “B.”
10* log (x/B) – 10* log (y/B)
= 10* log [(x/B) / (y/B)]
= 10* log (x/y)
= difference in dB
By golly… it works! You ecstatically wave your hands in the air, jump off your stool, cram the napkin intp your pocket, and impulsively kiss the waitress as you skip out the door. Everyone in the place now thinks you’re a nut.
Back at the lab, you’re now faced with the task of picking a good reference number. Looking over your experiments, you remember that the smallest intensity you found most people could hear was 0.000000000001 W/m2. How about using that as a reference? This way, any single measurement could be expressed in dB, as long as we always remember that we’re comparing it to 0.000000000001 W/m2 . You can see that your dB is still expressing a difference — there are, in fact, still two numbers involved. It’s just that the second number will just be an “implied” quantity of 0.000000000001 W/m2 .
You anxiously check it out to see if it works:
10* log ( .000792710162 / 0.000000000001) = 89 dB
10* log ( .000006288415 / 0.000000000001) = 68 dB
89 dB – 68 dB = 21 dB
Man… are you a genius or what? You’ve invented the decibel! Good for you. Just don’t go around getting a swelled head over it now.
======================
Do You Have the “Power” to Take the “Pressure?”
So, now you know the story of the decibel. To review:
The difference (in dB) between any two POWER measurements (let’s call them “x” and “y”) is
dB = 10* log (x/y)
There’s a darn good reason I put that word “POWER” in all capital letters. And here, we come to another crucial point — there is a distinct difference insound power (watts), sound intensity (watts per square meter), and sound pressure (Pascal). Hold on, I’ll explain what I mean in a minute. Pay close attention now; because this is a major source of confusion when it comes to decibels!
As long as we’re talking sound power (in watts) or sound intensity (watts per square meter), the formula given above is perfectly good. However, when you commonly hear the term “dB” bandied about in terms of “loudness of sound,” people usually aren’t talking about sound power or sound intensity, but more accurately sound pressure levels, or SPL. After all, it’s the pressure a sound exerts on our eardrums that determines how “loud” that sound is to us!
Sound power is measured in watts. Sound intensity, as we’ve already discovered, is the ratio of power over a given area, and is measured in watts per square meter (W/m2). Pressure, on the other hand, is a measure of force over a given area. Since force is expressed in Newtons (N), pressure can therefore be expressed as Newtons per square meter (N/m2). The more commonly used unit is the Pascal (Pa). (1 Pa is the same as 1N/m2 .)
The relationship between intensity (I) and pressure (P) is defined as
I = P 2/r
where r (the Greek letter rho) is “air impedance” — a constant which is determined by atmospheric pressure, air temperature, and so on. For normal conditions, and at room temperatures, the value of r is very close to 400. Therefore, the threshold intensity of hearing we mentioned before — .000000000001 W/m2 — correlates to a pressure reading of about .00002 Pa:
.000000000001 W/m2 = (.00002 Pa)2 / 400
At the other end of the scale, the threshold intensity of pain, given before as 1 W/m2 , correlates to a pressure of about 20 Pa:
1 W/m2 = (20 Pa)2 / 400
So, in terms of sound pressure levels, the range of human hearing is about .00002 Pa to 20 Pa.
There’s still one other thing to consider concerning the relationship between intensity and pressure. Notice that the intensity of a sound does not vary directly with pressure, but as the square of the pressure. Look at the formula again: I = P 2/r. Think about what is happening here. When pressure doubles, intensity quadruples. When pressure quadruples, intensity goes up by a factor of sixteen, and so on. Unfortunately, that means for pressure calculations, our old formula, dB = 10* log (x/y), won’t work any more!
Fortunately for us though, it should be too tough to “pressure” our equation into shape for our purposes!
dB = 10 * log (x/y), where “x” and “y” are measurements of sound intensity
Substituting the expression P 2/r for these intensity measurements, we get
dBspl = 10 * log [ (Px2/r) / (Py2/r) ]
= 10 * log (Px2/Py2)
= 10 * log (Px / Py)2
= 20 * log (Px/Py)
This is almost the same as our formula for power, except this time we have to multiply by 20 instead of 10.
It is this term — dBspl — that is being referred to about 99% of the time when you hear or read the term “dB” concerning the loudness of a sound. This is in fact exactly what you are measuring when you use a sound level meter — the pressure on the mic, referenced to .00002 Pa, and expressed in terms of dBspl. (Often, the dB reading shown on a meter is a weighted measurement; something we’ll explore more deeply in Part II of this article.) The problem is that almost nobody attaches the little “spl” to the end, which tends to make things needlessly confusing! When it comes to loudness, just remember that “dB” is just kind of understood in practice to mean “dBspl.”
The reference measurement against which SPL is measured is .00002 Pa, which is a good approximation of the lower threshold of hearing for most normal, healthy youths. That’s the figure to use for the bottom of the fraction in the formula above.
dBspl = 20 * log (Px/ .00002 Pa)
Since log 1 = 0, it doesn’t then take a lot of head scratching to figure out what the dB level of the smallest audible sound is, does it?
20 * log (.00002 Pa / .00002 Pa) = 0 dB SPL
Pay attention to that last equation, because it points up a neat-o property of the dB: Because log (1) = 0, any measurement that is equal to the reference measurement is always “0 dB,” regardless of the dB designation in question. This holds true for dBm, dBu, dBV, dBFS… it doesn’t matter. You see this more clearly in a moment.
The loudest sound pressure we can tolerate is about 20 Pa, as we’ve already noted. Can you figure out how to express this in terms of dB? If you’ve been following closely so far, it should be no sweat:
20 log (20 Pa / .00002 Pa) = 120 dB
So, now you know that the dynamic range of human hearing is approximately 120 dB. Actually, I’m sure you already knew that. But, now, you know why.
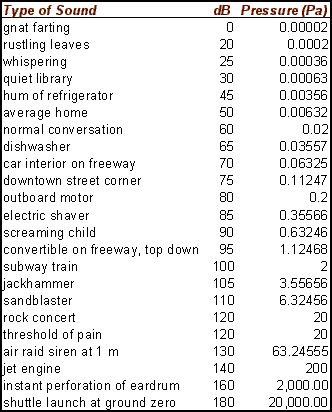
Of course, just about every other sound you can hear is going to fall somewhere in the range between 0 dB and 120 dB. Just for fun, I’ve included a handy-dandy table of common sounds, and their approximate loudness in dB (remember, in this table, dB means dBspl!)
The Secret’s in the Recipe… uh, I mean, Reference
To review so far:
1) The difference (in dB) between any two POWER measurements (let’s call them “x” and “y”) is
dB = 10* log (x/y)
2) The difference (in dB) between any two PRESSURE measurements (Let’s call them Px and Py) is
dB = 20 * log (Px / Py).
Okay… all well and good so far. But you know as well as I do that there’s more to this story. So, what you’re probably asking right about now is, “what’s the deal with all this dBu, dBv, dbV, dBm, dbVU, dBFS, and so on? Help me! I’m drowning in alphabet soup!”
Relax… once you understand what the term “decibel” really means, all the rest of this stuff is easy! Remember, the designation “dB” denotes a comparison between two numbers (of the same type, of course — you can’t use dB to directly compare, say, volts to watts). One of those numbers is usually a reference of some sort. That little bit on the end merely reminds us what’s being measured. The reference level to which various measurements are compared have become standardized over the years, as I’ll explain below.
dBm and dBVU
Now we’ve already discussed the derivation of dB as concerns power measurements. We talked about it in terms of sound power (measured in watts), but as we know, there are lots of other phenomena that can be discussed in terms of “power” — like electricity, for example.
Back in the good ol’ days, before LED ladders and fancy LCD displays and such, audio engineers relied on a device known back then (as it is today) as a VU meter. A VU meter is nothing very fancy; merely a cool little device consisting of a needle attached to a magnet, such that as the current in the magnet increases, the needle turns clockwise. “VU” stands for Volume Unit, a term developed during the early days of radio.
The problem with VU meters when they were first introduced was that all of them were different. That is, until the late 30s — when a bunch on engineers sat down and decided to standardize the VU meter such that whenever the power in a circuit was one milliwatt (1 mW rms), the VU meter would read 0 dB, or, in other words, 0 dBm = 0 dBVU.
The little “m” in dBm stands for milliwatt. The dBm is a measurement of power, always referenced to 1 mW.
dBm = 10 * log (Power / 1mW)
Knowing this, it’s pretty easy to express the power in a circuit in terms of dBm. You already know what happens when the power in the circuit is 1mW. This is the reference power level — and when a measurement is equal to the reference level, the formula always yields zero, remember?
10 * log (1 mW / 1mW) = 10 * log (1) = 0 dBm
As we’ve said, this is the reading that would normally cause a VU meter to read 0 dBVU. If you see that your VU meter jumps from 0 dBm to +3 dBm, you know that the power in the circuit has doubled, because
10 * log (2 mW / 1mW) = 10 * log (2) = 3 dBm
What if the needle drops from 0 dBm to -6 dBm? What is that telling us?
10 * log (0.25 mW / 1 mW) = 10 * log (.25) = -6 dBm
What’s happened in this case is that the power in the circuit has dropped to one-quarter of its previous value.
Now I would hate for you to think that every VU meter you see is graduated in dBm, for this is not the case! When other types of gear was invented, engineers decided to use VU meters for them as well, and calibrated the meters such that the measurement that was equal to the reference measurement would make the meter read 0 dBVU. Take the tape recorder for example. They put VU meters on tape recorders, but this time, instead of calibrating 0dBVU to an electrical power reference, they calibrated the meters to a magnetic power reference. Magnetic power, often referred to as flux, is expressed in Webers per meter (W/m). Since the magnetic flux of recording tape is pretty small (good thing, too — I’d hate to have my fillings sucked out by a reel of tape!) we usually use nanoWebers per meter (nW/m). A nanoWeber is one-billionth of a Weber.
The VU meters on a tape recorder were set to read 0 dBVU at whatever the recommended recording level of the tape was. The first recording tape put out by Ampex sounded pretty good at 185 nW/m, so those old Ampex machines used 185 nW/m as the 0 dBVU reference on the VU meter. The cassette standard is 160 nW/m, so the VU meters on a cassette deck are calibrated such that a flux of 160 nW/m on the tape causes the VU meter to read 0 dBVU. The dB meters on modern professional analog decks are calibrated to match the much hotter recording levels possible with today’s high-tech oxide formulations — 250 nW/m and up. The spec sheet on a particular deck will usually tell you how many nW/m “0 dBVU” means on that deck’s meters.
dBu (a.k.a. dBv)
Think back again to that high school physics class. We know from Watt’s Law that there is a relationship between power and voltage, don’t we? Watts Law states that
P = V2 / R
where P is the power in Watts (W), V is the electrical potential in Volts (V), and R is the resistance (or, in this case, impedance) in Ohms (W).
If you remember from our discussion of dBm, the reference power used in that case was 1mW. As I said, this standard was developed in the 1930s — and back then, the input impedance of every piece of audio gear made was 600 ohms, period. Tape decks, mixers, preamps, power amps, everything — if it had an input, the resistance from the hot wire to the ground connector was 600 W. That’s just the way things were back then!
So the question now becomes: What voltage does it take to generate 1 mW of power across a 600 W impedance?
P = V2 / R
.001 W = V2 / 600 W
V2 = .001 W * 600 W
V = sqrt (.001 W * 600 W)
V = .775 Volts
We see that it takes about .775 V to generate 1 mW of power at 600 W. Even though the 600 W impedance “standard” went the way of the dinosaur long ago, the .775 V reference remains as the reference voltage for dBu.
There’s one more very important detail to note here. Notice that power varies as the square of the voltage. This is the analogous situation to the dB derivation of sound pressure, given earlier. In fact, voltage can be (and often is) thought of as “electrical pressure.” If we do the same substitution calculation for voltage as we did for SPL, we get the “ times 20” formula
dBu = 20 * log (voltage / .775 V)
There’s something you may be wondering at this point — why the “u?” Well, it wasn’t always that way. The term “dBu” was originally written as “dBv” (with a small “v”), and in fact you’ll still see old-timers use “dBv” sometimes. The problem was that folks kept getting their “dBv” (small “v”) confused with “dBV” (capital “V”), and we can’t have that now, can we? So, “dBv” was changed to “dBu.” Just remember that if you ever see the term “dBv” being used anywhere, it means “dBu,” or that the person using it has fallen into the same small v-capital V confusion.
Speaking of which…
dbV
We’ve come a long way since the days when the impedance of gear was 600 W. On today’s stuff, you’re likely to encounter much higher impedances — 10,000 W or more. At impedances that high, power dissipation is pretty low (in fact, we’re talking microwatts here now) because impedance and power are inversely proportional (Watt’s Law again: P = V2 / R).
Remember that the dBu uses .775 V as a reference, which some engineers thought to be kind of awkward — and because the 600 W standard had been abandoned, there was no special significance to that .775V reference level any more. So, a new standard was developed — dBV — that instead, uses a nice, round, 1V as a reference instead.
dBV = 20 * log (voltage / 1V)
You can see that dBu and dBV are very similar! They both compare voltages; it’s just the reference levels that are different.
A side trip — “Professional” vs. “Consumer” Levels
There has always been a lot of confusion about the whole issue of the nominal operating level of “professional” gear versus the nominal operating level of so-called “consumer” gear.
You may have heard that professional gear is “+ 4 dBu” and consumer gear is “- 10 dBV.” Because only professionals used this stuff back when it was new (and expensive!) technology, and the older dBu designation was all they had to work with, the original designation of operating level (expressed in dBu) has stuck. By the time consumer audio products were introduced in a big way, the dBV has been invented, and so dBV was used for consumer gear. (Remember, they are both simply ways of comparing voltage levels — nothing more. That + 4dBu is somehow inherently “better” than -10 dBV is a big, fat myth, kept alive by the somewhat arbitrary labels of “professional” and “consumer” attached to them.)
I’ll just bet that a lot of you have glanced at this “+4 / -10” thing, and just assumed that the difference between the levels is 14 dB. But now we know better, don’t we?
The reason the difference isn’t 14 dB is because the reference levels between dBu and dBV are different! Remember, dBu is referenced to a voltage level of .775 V, and dBV is referenced to 1V. Armed with the knowledge you now possess, can you figure out what the true difference in operating level is, between + 4 dBu and -10 dBV?
+ 4 dBu = 20 * log (voltage / .775 V)
voltage = 1.228 Volts
– 10 dBV = 20 * log (voltage / 1V)
voltage = 0.3162 Volts
20 * log (1.228V / 0.3162V) = 11.79 dB
You can confirm this by doing a little experiment. Plug a piece of consumer gear with -10 dBV outputs into a piece of gear with + 4 dBu inputs. If they both have VU meters, calibrated such that 0dBVU on each piece of gear corresponds to it’s nominal operating level, you’ll find that 0dBVU on the consumer gear causes a reading of -11.79 dBVU on the pro gear’s meters.
dBFS
We now come to a relatively new, yet all-important dB designation, the “dBFS,” which stands for “decibels full scale” — a kind of dB designation created especially for digital gear.
This one is a little strange because, unlike all the other dB varieties, the reference level isn’t at the bottom, or somewhere near the middle, but at the very top possible measurement. This means that “0 dBFS” designates the highest possible level, and that all other measurements expressed in terms of dBFS will always be less than 0 dB — in other words, a negative number. This is why, on digital gear using VU meters (where 0 dBVU means 0 dBFS), the “0” is at the top of the scale, and the meter can never read higher than that.
Let’s take16 bit digital audio as an example. “The term “16-bit” means that the level of any sample can be stored as a 16-bit binary number (a binary number with 16 placeholders). As we know, the binary number system only has two digits, “0” and “1.” Therefore, the highest possible 16 bit binary number is the number with all “1”s: 1111 1111 1111 1111 (binary). So the formula for dBFS in a 16 bit digital system is:
dBFS = 20 * log (sample level / 1111 1111 1111 1111)
It’s easy to see why they say “you can’t go over 0 dB in digital.” That’s because, at the highest possible sample level (which is the dB reference level, in the case of digital):
20 * log (1111 1111 1111 1111 / 1111 1111 1111 1111) = 0 dBFS
Also, using the same formula, we can easily figure out the dynamic range of a 16-bit system, because we know the smallest possible sample level (other than zero, of course) is 0000 0000 0000 0001.
20* log (0000 0000 0000 0001 / 1111 1111 1111 1111) = -96 dB
So, now you know why the meters on a 16-bit DAW usually read from 0 dB to -96 dB, when displayed at their highest resolution. By following the same logic, it’s easy to figure out that the dynamic range of a 20-bit digital audio system is 120 dB, and that for 24-bit digital audio, it’s 144 dB. I’ll let you do the math if you want to. (Hint: on most calculators, it’s easier to convert the binary numbers to decimal numbers first — otherwise, you’re likely to run out of digits!)
Coming in Part Two
This concludes our discussion on the mighty decibel, at least for now. In the second and final installment of this article, we’ll talk about weighted decibel measurements, which are an attempt to more closely associate raw dBspl readings with the way humans actually hear sound. We’ll figure out some handy rules-of-thumb concerning decibels, and pull off a few Stupid Decibel Math Tricks. I’ll also help you solve the rest of those brain teasers at the beginning of this article. (You won’t want to miss that, huh?) Of course, if you feel ambitious, there’s no need to wait for me — feel free to go ahead and get started on them now. The article you just read presents all the knowledge required!
I’ll leave you with a handy Decibel Cheat Sheet. You might even want to print it out and hang it on your fridge!

Until next time… happy dBs!
Lionel Dumond is the Managing Engineer at Sweetwater Sound Productions in Fort Wayne, Indiana, and is the Media and Mastering Editor here at ProRec. Unfortunately, he wasn’t able to successfully explain the decibel system to the cop who wrote him the ticket for the cherry bomb mufflers on that ‘68 Mustang…